Para el procesamiento de la serie se utilizan varios métodos: los habituales y otros más complejos como, por ejemplo: el alisamiento exponencial, funciones de regresión (mínimos cuadráticos) y métodos multivariantes (ARIMA).

En nuestro estudio nos referiremos a los métodos habituales. Los métodos más complejos se pueden consultar en diferentes textos de bioestadística y epidemiología.

Comenzaremos con el estudio de las variaciones estacionales y la tendencia.

Variación estacional.

Entre los métodos habituales se encuentran:

• Curvas de expectativas.
• Limites de variación habitual. (Canal endémico).

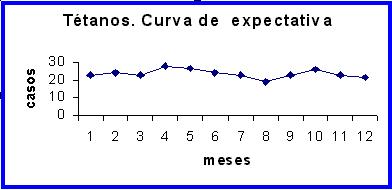
1- Las curvas de expectativas, para su cálculo tomaremos como ejemplo la construcción de la curva con la mediana, aunque existen cuatro formas más de calcularla (curva con el promedio, mediana y promedio móviles, mediana y valor último y promedio tricentral).

Curva con la mediana: se ordenan las cifras de los doce meses o 52 semanas de los años con que contamos, del mayor número al menor o a la inversa, es decir, todos los enero, febrero, semana 1, semana 2, etc. Si el número de años es impar la mediana será el valor central que dejará igual número de cifras por encima o por debajo, por ejemplo: si es 7, la mediana sería el valor ubicado en la cuarta posición, dejando tres cifras por debajo y por encima, estos valores centrales que se obtienen por meses o por semanas se inscriben en un gráfico, correspondiendo al índice endémico. Si contamos con números de años pares se puede realizar la semisuma de los dos valores centrales una vez ordenados los valores como se explicó en el caso anterior. Veamos un ejemplo.

Notificación de casos de tétanos. Cuba 1965-1973.

                      FUENTE: Tejeiro. : Rev. Cub. Adm. Salud, v(1):60, 1975.

A continuación veremos los datos ordenados de mayor a menor:

                   FUENTE: Tejeiro.Rev. Cub. Adm. Salud, v(1):60, 1975.

Con los valores correspondientes al centro se prepara el gráfico 1 y que se corresponden con la mediana. Ya se podrán ubicar los datos por meses del año 1974 para ver cómo se comportan los datos con relación a la estacionalidad.

Límites de variación habitual: en este caso se trae como ejemplo, la construcción del canal endémico, el cual es de mucha más utilidad que la curva de expectativas cuando se realizan actividades de vigilancia.

Para la construcción del canal se pueden emplear diferentes métodos entre los que se encuentran:

1. Canal del máximo-maximorum y del minimo-minimorum: este se utiliza cuando se tienen pocos años y no se puede desechar información 6-7 años, en este caso se ordenan los números como ya explicamos y se obtienen la mediana y los números de la línea superior y la inferior. Posteriormente se inscriben en el gráfico la mediana y los números de la línea superior e inferior de la tabla.
2. Canal endémico utilizando las cifras inframáximas y supramínimas, en este caso se necesitan más de 9 años, pues se eliminarán las líneas extremas, lo que permite excluir una buena parte de las cifras aberrantes, el procedimiento general es similar al ya explicado.
3. Canal endémico utilizando la mediana y la desviación estándar, se obtiene la mediana y se calculan los datos con más dos desviaciones estándar y con menos dos desviaciones estándar, en ese intervalo se agruparán alrededor del 95% de los casos esperados, finalmente se inscriben los datos obtenidos en un gráfico.

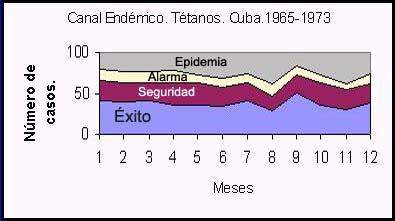
En todos los casos la curva demostrará 4 áreas y se podrá apreciar si los datos del año que se está vigilando se encuentran por debajo o por encima de lo esperado.

A las cuatro áreas se les llama, de abajo hacia arriba, éxito, seguridad, alarma y de epidemia. A continuación se le ofrece el ejemplo anterior utilizando el método del inframáximo y supramínimo.

Tendencia.

Este componente de la serie también se conoce como tendencia histórica, evolución histórica y tendencia a largo plazo. En el análisis de su comportamiento no hay un valor normal del que se parte para comparar las variaciones, lo que se busca es la dirección, inclinación o tendencia en la evolución del evento objeto de vigilancia. Solo existen cuatro grandes posibilidades de resultados. La tendencia es ascendente, descendente, estacionaria o presenta grandes oscilaciones.

Para su análisis se utilizan métodos matemáticos simples y complejos y métodos gráficos.

En el primer caso se encuentran cinco métodos de análisis matemático simple, mientras que los que requieren de mayor procesamiento estadístico se pueden encontrar en los libros especializados.

MÉTODOS MATEMÁTICOS SIMPLES.

1. Diferencia absoluta.
2. Cambio relativo.
3. Diferencias absolutas o cambios relativos de grupos de valores extremos.
4. Números índices.
5. Promedio de cambio.

En esta oportunidad se explicarán los primeros tres ejemplos

• En el caso del método por diferencia absoluta se procederá a calcular la diferencia que existe entre los valores extremos de una serie, por ejemplo: atenciones médicas por EDA en menores de un año, en la ciudad Amatista de 1993 a 2002.

Año 1993- 38 845
Año 2002- 26 557

Cálculo: 38 845 - 26 557= 12 288

Interpretación: Entre el año 1993 y el 2002 se reportaron 2 002 atenciones médicas menos por EDA entre la población menor de 1 año de la Ciudad Amatista.

• Si utilizamos el método de cambio relativo se considera el primer año como el 100 %, calculándose por una regla de tres el porcentaje que le corresponde al último año. Utilizaremos el mismo ejemplo.

Atenciones médicas por EDA en menores de 1 año, en la Ciudad Amatista. 1993- 2002.

Cálculo.

Año 1993- 38 845
Año 2002- 26 557

38 845--- 100%
26 557--- X

X = 68,3%.
100 - 68,3 = 31,7%

Interpretación: En el año 2002 se brindaron en la Cuidad Amatista 26 557 de atenciones médicas por EDA, lo que representan el 68,3% de lo atendido en el año 1993. En general se disminuyó en un 31,7% las atenciones médicas por EDA en este período.

Estas dos formas de calcular la tendencia se pueden utilizar en eventos que presenten una tendencia muy bien definida.

En el caso del método de las diferencias absolutas o cambios relativos de grupos de valores extremos se procede de la siguiente manera:

Se calcula la diferencia absoluta entre el primer grupo de años y el segundo: 35 626 – 31 107 = 4 519.

Interpretación: en el período estudiado los cambios relativos de los valores extremos fueron 4 519 atenciones médicas por EDA menos entre los menores de un año de la ciudad Amatista.

Para el cambio relativo se considera el primer grupo de años como el cien porciento calculándose entonces lo que representa la diferencia encontrada.

35 626 ---- 100%
4519 ---- X

X = 451 900/ 35 626 = 12,7%

Interpretación: el cambio relativo de valores extremos, en la década comprendida entre 1993 y 2002 fue de 12,7 % de atenciones médicas por EDA en menores de 1 año en la Ciudad Amatista. Este método se usa para series irregulares, es decir cuando existen fluctuaciones de la serie

MÉTODOS GRÁFICOS

1. Línea a mano alzada.
2. Semipromedio
3. Ciclo medio
4. Medianas móviles
5. Promedios móviles

En nuestro trabajo nos referiremos a dos formas de inscribir la tenencia de manera gráfica: línea a mano alzada y el método de los semipromedios.

Método de línea a mano alzada: es el más sencillo y se traza la tendencia observando los datos del gráfico.

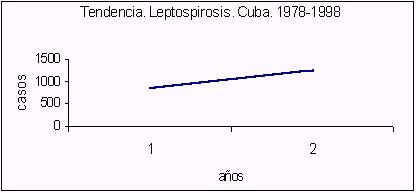
En el caso de los semipromedios se obtiene a través del cálculo de los promedios, se divide la serie en dos y se haya el promedio de cada una. Cada promedio se inscribe en la mitad del tiempo que corresponde en la abscisa o años tomados y se unen por una línea recta. Si los años son pares se calcula el promedio con las dos mitades, si son impares el número central se incluye en cada semisuma y se promedian. Por ejemplo: casos notificados de leptopirosis en Cuba de 1978 a 1998.

            Casos notificados de Leptospirosis. Cuba 1978-1998.

                Fuente: Anuario estadístico 1998

La media de los primeros 10 años sería de 319,6 y la del segundo de 1146,8.
Veremos cómo se observa la leptospirosis en el tiempo y su tendencia de manera gráfica.

Al trabajar la tendencia como componente de la serie es muy frecuente calcular o construir un pronóstico

¿ Qué cosa es un pronóstico?

Es una estimación de una o varias variables que conforman la estructura de un evento futuro en base a la información actual y/o pasada.

La palabra pronóstico se deriva del latín prognosticum y este del griego (prognostikon o progignosko) que significa “yo conozco de antemano”.

Tipos de pronósticos:

• Pronósticos a largo o corto plazo.
• En términos de su posición en el entorno micro-macro económico.
• De acuerdo a su tendencia a ser más cuantitativos o cualitativos.

Etapas en la realización de un pronóstico:

• Obtención de datos.
• Reducción y condensación de los datos.
• Construcción del modelo.
• Extrapolación del modelo (el pronóstico en sí).

El propósito del pronóstico consiste en reducir el margen de incertidumbre dentro del que se deben efectuar los juicios de la administración.

Para una buena selección de la técnica de pronóstico el pronosticador deberá hacer lo siguiente:

• Definir la naturaleza del problema de pronóstico.
• Explicar la naturaleza de los datos bajo investigación.
• Describir las capacidades y limitaciones de las técnicas de pronóstico potencialmente útiles.
• Desarrollar algunos criterios predeterminados sobre los cuales se pueda tomar la decisión de la selección.

Un factor principal que influye en la selección de una técnica de pronóstico consiste en la identificación y comprensión de patrones históricos en los datos. Si se pueden reconocer patrones de tendencia, cíclicos o estacionales, entonces se pueden seleccionar las técnicas con la capacidad de utilizar eficazmente estos patrones.

Los elementos deseables en un pronóstico incluyen los siguientes:

• Precisión.
• Una medida de confiabilidad (previa).
• Reproductibilidad.

Clasificación de acuerdo al tipo de información que arrojan:

Cuantitativos .

• Determinísticos.
• Probabilísticos
  

A su referencia al tiempo:

• Estáticos.
• Dinámicos.
• Estructurales (regresión).
• Modelos de series de tiempo

Cualitativos:

• Estudio de caso.
• Lluvia de ideas.
• Panel de expertos.
• Delphi.
• Árboles de decisión.
• Planeación prospectiva

Los métodos cualitativos de pronósticos utilizan el juicio de las personas, su experiencia, los datos relevantes y un modelo matemático implícito.

Los pronósticos cualitativos deben utilizarse cuando los datos del pasado no resulten confiables como indicadores de las condiciones del futuro. También para la introducción de nuevos productos cuando no se dispone de una base de los datos históricos. Los métodos cualitativos casi siempre se utilizan para pronósticos a mediano y largo plazo. En el caso de estas decisiones, los datos del pasado casi nunca están disponibles o, cuando así es, pueden indicar un patrón poco estable.

Recapitulando, el pronóstico debe ser técnicamente correcto y producir predicciones lo más precisas posibles, de modo que los pronósticos se utilicen en el proceso de toma de decisiones en beneficio de la salud de las poblaciones; también los resultados deben ser justificados con base en su costo beneficio.

Se realiza su interpretación a través de la consolidación y presentación de los datos colectados en cuadros, gráficos o mapas, que pueda facilitar su análisis o interpretación.

Los datos deberán proyectarse en la unidad espacial más pequeña posible que permita el análisis de las variables, se debe realizar por grupos de edades y otras variables según el evento objeto de vigilancia, comparándolo con otros períodos en la misma localidad, y con diferentes períodos en diferentes localidades, aplicando para esto el análisis por tasas. Ello permitirá acercarse al riesgo real a que está expuesta la población, además de permitir la comparación de los datos obtenidos.

A continuación se muestra la variable espacio y su representación gráfica de la mortalidad infantil. País Esmeralda, 1998. La del país fue de 7,1 por cada 1 000 nacidos vivos.

En la distribución espacial aparecerán diferenciadas con color rojo aquellas provincias que se encuentran por debajo del índice nacional y azul por encima El análisis de los datos por espacio permitirá dirigir las acciones hacia aquellas regiones que presentan un comportamiento más desfavorable.